Algorithmes de résolution
Il existe de nombreuses méthodes pour résoudre le Rubik’s Cube.
Elles possèdent différentes caractéristiques, et sont dédiées à différents usages :
-
Certaines sont faciles à apprendre.
-
Certaines permettent de résoudre le cube rapidement.
-
Certaines sont applicables à plusieurs tailles de cubes.
-
Certaines permettent de résoudre le cube en peu de mouvements.
Deux méthodes sont actuellement implémentées sur CubeSolver :
-
La méthode de Jessica Fridrich, implémentée avec recherche de solution par population évolutive.
-
La méthode de Thistlethwaite.
Après avoir présenté le fonctionnement de ces deux algorithmes, leurs performances seront étudiées et comparées.
Algorithme évolutif / recherche d’OLL et de PLL exhaustive
La méthode appliquée est la méthode de Jessica Fridrich. La seule différence est que les coins du premier étage et les arêtes du deuxième étage sont résolus en deux temps, et non en un seul. (Pas de F2L pour les connaisseurs)

Les étapes de la résolution
Les différentes étapes sont donc :
- N’importe quel cube mélangé
- Un cube avec la croix blanche résolue
- Un cube avec le premier étage résolu
- Un cube avec les deux premiers étages résolus
- Un cube avec les deux premiers étages résolus, et les pièces du dernier étage bien orientées
- Un cube résolu
La résolution des deux premiers étages se fait grâce à un algorithme évolutif, le dernier étage est résolu par une recherche exhaustive dans une série de séquences.
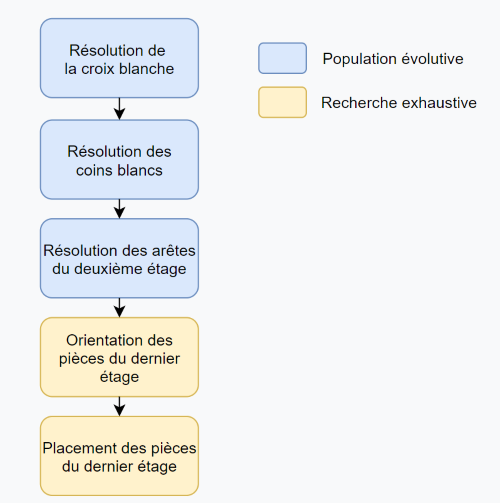
Processus de résolution du cube
Résolution des deux premiers étages par population évolutive
Il s’agit là du premier algorithme de résolution que j’ai implémenté, il s’inspire d’un algorithme génétique sans en être un.
Pour rappel, voici le résumé schématique du fonctionnement d’un algorithme génétique :
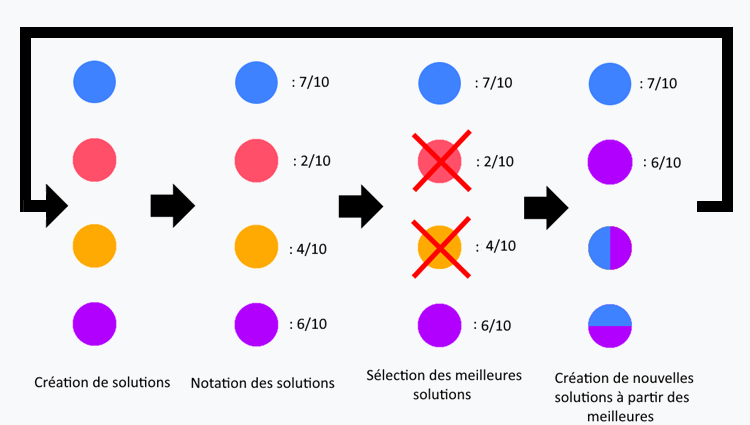
Fonctionnement d’un algorithme génétique
Les principaux choix liés au développement d’un tel algorithme concernent :
- La création d’une heuristique permettant de noter chaque solution.
- La quantité « d’individus » à conserver à chaque itération.
- La manière dont de nouvelles solutions peuvent être créées à partir des anciennes.
Pourquoi ne pas appliquer directement un algorithme génétique ?
Il est difficile d’appliquer un tel algorithme à la résolution d’un Rubik’s Cube à cause de la dernière étape, également nommée « cross-over ».
Pour créer un nouvel individu grâce à deux parents, il faut mélanger les « gènes » de ces deux parents. Ces gènes peuvent être de différentes natures selon le problème (comme par exemple des nombres que l’on peut moyenner), mais dans notre cas, rappelons que chaque solution est une séquence de mouvements.
Ici, les mouvements qui composent ces solutions n’ont du sens qu’au sein de leur séquence.
Si la séquence 1 – 2 – 3 – 4 est prometteuse
Ainsi que la séquence 9 – 8 – 7 – 6
Je n’ai aucune garantie que la séquence 1 – 8 – 3 – 6 ou même 1 – 2 – 7 – 6 soit intéressante.
Ainsi, appliquer un cross-over aux solutions, et donc « mélanger » deux parents, semble difficile.
A la place, il est possible de rajouter des éléments aléatoires à la fin d’une séquence intéressante.
Par exemple, si la séquence 1 – 2 – 3 – 4 a de bons résultats, on peut essayer la séquence 1 – 2 – 3 – 4 – 9.
On « repeuple » ainsi notre ensemble de solutions en ajoutant des éléments aléatoires aux solutions précédemment sélectionnées.
Voilà pour le fonctionnement de cet algorithme.
L’implémentation est disponible ici.
Chacune des itérations est décomposée en trois étapes :
- On note chacun des individus de notre population.
- On sélectionne les meilleurs individus.
- On recrée une population à partir des survivants. Et l’algorithme s’arrête lorsqu’un individu parvient à atteindre l’objectif.
L’heuristique (la méthode de notation des individus) dépend des étapes de la résolution.
L’objectif est de récompenser les individus s’approchant de la solution, on peut donc donner des points à une séquence lorsque certaines pièces se trouvent à certains emplacements.
Nous avons trois paramètres pour notre algorithme :
- Quelle est la taille de notre population ?
- Combien d’individus sélectionne t’on à chaque itération ?
- Lorsque nous créons de nouveaux individus, combien de mouvements ajoute t’on ?
Résolution du dernier étage par recherche exhaustive
Le nombre de séquences possibles pour orienter et permuter les pièces du dernier étage est très faible (57 pour l’orientation et 21 pour la permutation).
Ainsi, tester toutes ces séquences (stockées en dur dans le code) nous garantis de résoudre le dernier étage rapidement, et simplement.
Cette méthode est directement issue de la méthode de Jessica Fridrich, l’utilisation de ces 78 séquences est classique dans le milieu du speedcubing.
Elles ont donc un nom : OLL (Orientation of Last Layer) et PLL (Permutation of Last Layer), vous pouvez trouver toutes les informations les concernant ici et ici.
L’implémentation est disponible ici.
Algorithme de Thistlethwaite
Morwen Thistlethwaite est un mathématicien britannique ayant développé une solution célèbre pour le Rubik’s Cube.
Cet algorithme est constitué de plusieurs étapes, et chacune d’elles consiste à amener le cube dans une position où il peut être résolu en utilisant un sous-ensemble de mouvements. Ainsi, à chaque étape, le nombre de configurations possibles du cube diminue, jusqu’à atteindre l’état final.
Cet article est illustré avec un exemple de résolution. Voici le cube qui sera résolu :

Un cube mélangé
Et voici le mélange associé à ce cube : [D, F’, R2, B2, R, U’, D2, F2, L2, U’, F2, L, D’, L, B’, F’, R, D']
Première étape :
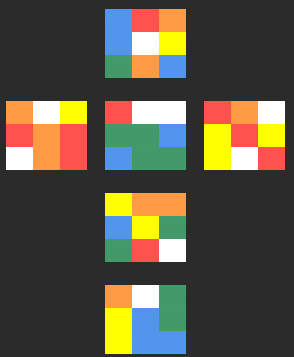
Résolution de la première étape
Solution: [B, R’, D’, L’, U']
Objectif: Orienter les douze arêtes du Rubik’s cube.
Espace de recherche: <L, R, F, B, U, D>
Réduction de l’espace de recherche: On cesse d’utiliser les quarts de tour de la face U (Up) et D (Down).
En effet, une arête est dite bien orientée s’il est possible de la résoudre sans utiliser les quarts de tours de la face du haut, et de la face du bas. Une fois que toutes les arêtes sont bien orientées, il est possible de résoudre le cube sans utiliser ces deux mouvements et on peut donc les ignorer.
Deuxième étape :
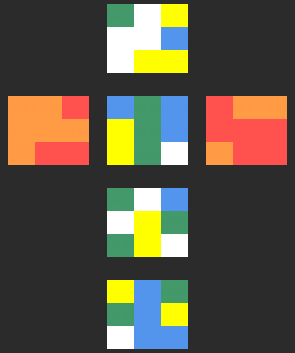
Résolution de la deuxième étape
Solution: [B’, D2, R’, F’, L’, F’, R’, B']
Objectif: Orienter les huit coins du Rubik’s cube, et regrouper toutes les arêtes de la tranche M dans la tranche M.
Espace de recherche: <L, R, F, B, U2, D2>
Réduction de l’espace de recherche: On cesse d’utiliser les quarts de tour de la face F (Front) et B (Back).
Un coin est dit bien orienté si sa couleur L / R est présente sur sa face L / R. Lorsqu’on cessera d’utiliser les quarts de tours des faces F / B, il sera impossible de modifier l’orientation des coins, qui resteront donc dans leur bonne orientation jusqu’à la fin de la résolution.
La tranche M est celle qui se situe entre les faces L / R. De même, une fois les arêtes M placées dans la face M, elles ne pourront plus en sortir puisqu’on arrêtera d’utiliser les quarts de tours de la face F / B.
Troisième étape :
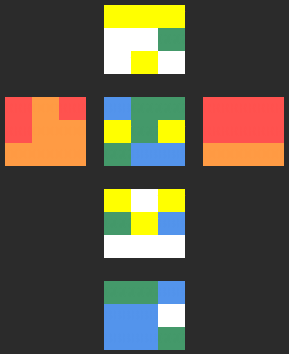
Résolution de la troisième étape
Solution: [R2, B2, R, D2, R']
Objectif: Amener chaque coin dans son « orbite naturelle ».
Espace de recherche: <L, R, F2, B2, U2, D2>
Réduction de l’espace de recherche: /
Un coin est dit « placé dans son orbite naturelle », s’il peut être résolu en utilisant seulement des doubles mouvements. (L2, R2, F2, B2, U2, D2)
Il n’existe que 96 positions de coins correspondant à cette exigence.
Quatrième étape :

Résolution de la quatrième étape
Solution: [B2, R’, B2, D2, B2, U2, D2, L']
Objectif: Amener chaque arête dans sa tranche finale
Espace de recherche: <L, R, F2, B2, U2, D2>
Réduction de l’espace de recherche: On cesse d’utiliser les quarts de tours des faces L / R.
Une fois les arêtes de chaque tranche (M, E, et S) amenées dans leur tranche finale, elles peuvent ainsi être résolues en utilisant uniquement des doubles mouvements.
Cinquième étape :
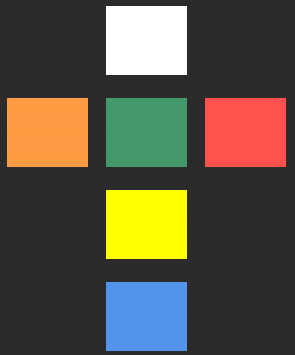
Fin de la résolution !
Solution: [R2, U2, R2, U2, R2, F2, D2, F2, R2, B2, D2]
Objectif: Résoudre le Rubik’s cube
Espace de recherche: <L2, R2, F2, B2, U2, D2>
Le cube peut désormais être résolu en utilisant uniquement des doubles tours, et une solution peut être trouvée relativement rapidement.
L’implémentation :
Mon implémentation de cet algorithme est disponible ici.
L’algorithme de recherche de solution utilisé est IDDFS (Iterative Deepening Depht First Search).
Il s’agit d’un algorithme dérivé du DFS, parcourant les solutions dans un ordre similaire à celui d’un BFS.
Performance des algorithmes
Définition de la performance :
La performance des algorithmes peut être définie selon deux critères :
- La vitesse moyenne de résolution d’un cube.
- Le nombre de mouvements moyen nécessaires pour une résolution.
L’importance de l’implémentation :
La vitesse d’exécution d’un algorithme dépend grandement de la qualité de son implémentation.
Pour obtenir les meilleures performances possibles, il convient d’optimiser les parties critiques du code et l’architecture de nos données.
Afin de réaliser cette optimisation, nous pouvons utiliser un CPU Profiler.
Cet outil permet de déterminer en temps réel quelles sont les parties de notre code qui consomment le plus de ressources. Le travail du développeur est ainsi grandement facilité, puisqu’il peut concentrer son attention sur les éléments importants.
Performance des algorithmes :
Nous pouvons constater que l’algorithme de Thistlethwaite est bien plus long à exécuter, mais permet d’obtenir des séquences bien plus courtes.
Toutes les valeurs présentées ci-dessous sont des moyennes sur 100 résolutions.
Algorithme de Thistlethwaite :
Temps moyen de résolution : 253,34637 secondes. (4 minutes 13 secondes)
Nombre moyen de mouvements : 36.23 mouvements.
Algorithme évolutif
- Taille de la population : 100
- Pourcentage de population survivante : 10
- Nombre de mutations aléatoire : entre 1 et 5
Temps moyen de résolution : 0.36 secondes
Nombre moyen de mouvements : 101
Un examen plus poussé des performances sera disponible sur une prochaine version du site.